[Time Series] 시계열 예측의 기초: MA, ARMA, ARIMA 모델 완벽 가이드 - 1탄 SMA & EMA

안녕하세요, 데이터 과학과 금융 분석에 관심 있는 여러분! 오늘은 시계열 예측에서 중요한 역할을 하는 MA(이동 평균), ARMA(자기회귀 이동 평균), ARIMA(자기회귀 누적 이동 평균) 모델에 대해 알아보려고 합니다. 이 모델들은 복잡한 시장 데이터의 패턴을 이해하고 미래의 트렌드를 예측하는 데 큰 도움이 됩니다. 이 글을 통해 각 모델의 기초와 활용 방법을 이해하고, 여러분의 데이터 분석 능력을 한층 더 향상시킬 수 있기를 바랍니다.

타임시리즈 데이터

---

간단한 이동 평균(Simple Moving Average, SMA)의 계산

• 간단한 이동 평균(Simple Moving Average, SMA): 최근 n개 관측치의 평균을 계산하는 방법입니다. 이를 통해 데이터의 단기 변동을 평활화하고 추세를 파악할 수 있습니다.

SMA Formula

 

출처: https://medium.com/coinmonks/simple-moving-average-sma-and-exponential-moving-average-ema-in-quantitative-finance-10950040dd06

 

엔비디아(NVIDIA) 주간 주식 가격 데이터로 SMA 계산 예시

• 예를 들어, 엔비디아(NVIDIA)의 주간 주식 가격 데이터를 사용하여 SMA를 계산해보겠습니다. 이를 위해 Python의 yfinance 라이브러리를 사용할 수 있습니다.

import yfinance as yf
import matplotlib.pyplot as plt

# 엔비디아 주식 데이터 가져오기
nvidia = yf.download('NVDA', start='2023-01-01', end='2023-07-01', interval='1wk')

# 간단한 이동 평균 계산
nvidia['SMA'] = nvidia['Close'].rolling(window=5).mean()

# 차트 그리기
plt.figure(figsize=(10,6))
plt.plot(nvidia['Close'], label='엔비디아 주식 가격 (NVIDIA Stock Price)')
plt.plot(nvidia['SMA'], label='간단한 이동 평균 (SMA)', linestyle='--')
plt.legend()
plt.xlabel('날짜 (Date)')
plt.ylabel('가격 (Price)')
plt.title('엔비디아 주식 가격과 간단한 이동 평균 (NVIDIA Stock Price and Simple Moving Average)')
plt.show()

 

엔비디아 주가 가격과 간단한 이동평균

이 코드는 엔비디아 주식의 종가 데이터에 대해 최근 5주 간의 간단한 이동 평균을 계산하고, 이를 주식 가격과 함께 차트에 표시합니다. 이를 통해 주식 가격의 단기적인 추세와 변동을 쉽게 파악할 수 있습니다. 📊📈

 

이와 같이, 시계열 데이터를 분석할 때 이동 평균 모델은 중요한 도구입니다. 특히, 간단한 이동 평균(SMA)는 데이터의 변동성을 평활화하고 기저에 있는 추세를 드러내는 데 유용하게 사용됩니다. 이러한 기술은 금융, 경제, 기상학 등 다양한 분야에서 시간에 따른 데이터의 변화를 예측하고 분석하는 데 활용됩니다. 📉💹

 

이렇게 시계열 데이터 분석과 이동 평균 모델에 대해 알아보았습니다. 이러한 기본적인 방법론은 데이터 분석가, 투자자, 경제학자 등 다양한 분야의 전문가들에게 필수적인 도구로 활용될 수 있습니다. 🌟🔍📈

---

지수 이동 평균(Exponential Moving Average, EMA)의 개념

 

지수 이동 평균(Exponential Moving Average, EMA): 최근 관측치에 더 많은 가중치를 부여하는 이동 평균의 한 형태입니다. 이 방법은 최근의 데이터 포인트가 이전 데이터 포인트보다 더 중요하다고 가정합니다.

출처: https://medium.com/coinmonks/simple-moving-average-sma-and-exponential-moving-average-ema-in-quantitative-finance-10950040dd06

 

 

엔비디아(NVIDIA) 주간 주식 가격 데이터로 EMA 계산 예시

• 예시로, 엔비디아(NVIDIA)의 주간 주식 가격 데이터를 사용하여 EMA를 계산해보겠습니다. Python의 yfinance 라이브러리를 사용하며, ewm 메소드를 활용하여 EMA를 계산합니다.

import yfinance as yf
import matplotlib.pyplot as plt

# 엔비디아 주식 데이터 가져오기
nvidia = yf.download('NVDA', start='2023-01-01', end='2023-07-01', interval='1wk')

# 지수 이동 평균 계산 (alpha는 평활 인자)
nvidia['EMA'] = nvidia['Close'].ewm(alpha=0.1, adjust=False).mean()

# 차트 그리기
plt.figure(figsize=(10,6))
plt.plot(nvidia['Close'], label='엔비디아 주식 가격 (NVIDIA Stock Price)')
plt.plot(nvidia['EMA'], label='지수 이동 평균 (EMA)', linestyle='-.')
plt.legend()
plt.xlabel('날짜 (Date)')
plt.ylabel('가격 (Price)')
plt.title('엔비디아 주식 가격과 지수 이동 평균 (NVIDIA Stock Price and Exponential Moving Average)')
plt.show()

 

 

Alpha = 0.1 vs. Alpha = 0.7

 

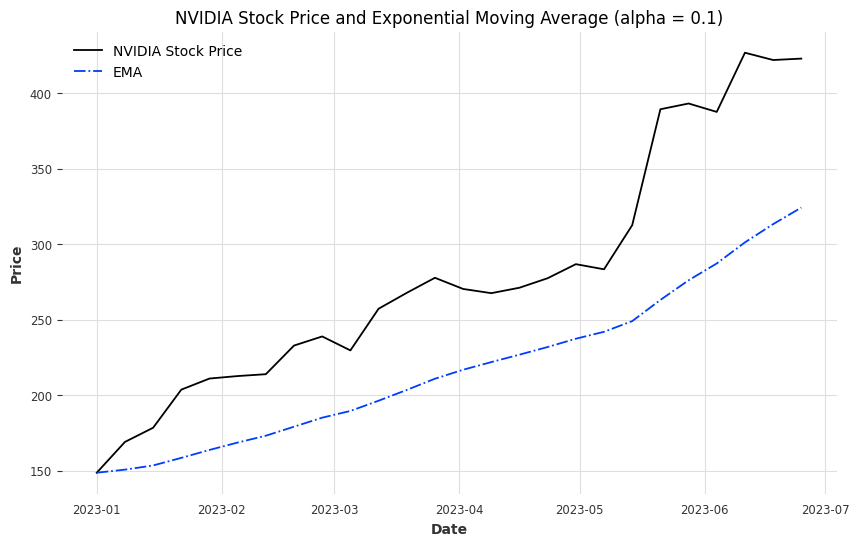
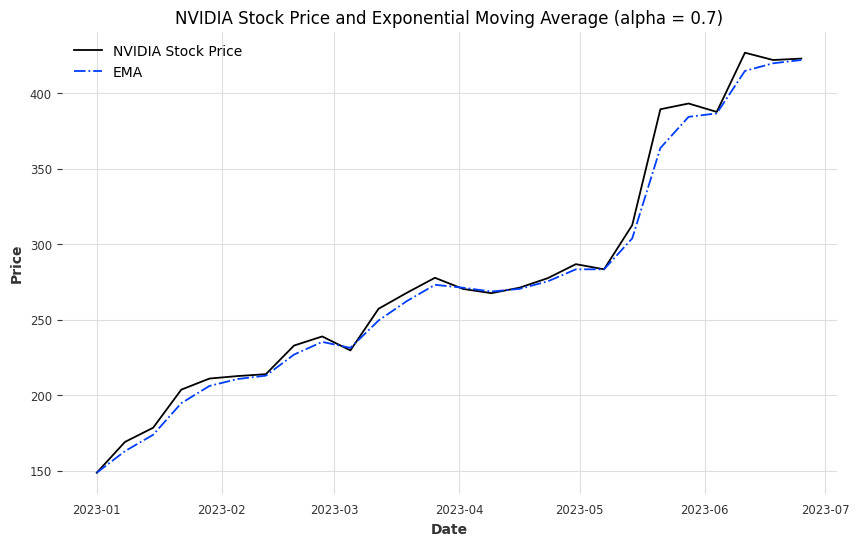
이 코드에서는 `ewm` 메소드의 `alpha` 매개변수를 사용하여 평활 인자를 조정합니다. `alpha` 값은 최근 관측치에 부여되는 가중치의 크기를 결정하며, 이 값이 클수록 최근 데이터에 더 큰 가중치를 부여합니다. 위 예시에서는 `alpha`를 0.1로 설정했습니다.

차트를 통해 볼 때, EMA는 주식 가격의 최신 변화에 더 빠르게 반응하여, 주가의 단기적인 추세를 파악하는 데 도움을 줍니다. EMA는 SMA에 비해 최근 가격 변동에 더 민감하게 반응하므로, 단기적인 가격 변동 추세를 포착하는 데 특히 유용합니다.

EMA는 금융 분석, 특히 주식 시장 분석에서 널리 사용되며, 트레이더들은 EMA를 사용하여 진입 및 탈출 시점을 결정하는 데 도움을 받기도 합니다. 시장의 단기적인 움직임을 파악하는 데 있어, 지수 이동 평균은 매우 중요한 도구로 활용됩니다. 📊🚀💹

---

 

오늘 우리는 시계열 예측의 기본이 되는 MA, ARMA, ARIMA 모델에 대해 배웠습니다. 이러한 모델들은 경제, 금융, 기상학 등 다양한 분야에서 데이터의 시간적 변화를 분석하고 예측하는 데 사용됩니다. 이 글이 여러분이 시계열 데이터를 더 깊이 이해하는 데 도움이 되었길 바라며, 앞으로도 데이터 과학의 흥미진진한 여정에 함께해 주시기를 바랍니다. 데이터 분석의 세계에서 계속 새로운 지식을 탐험해 보세요!